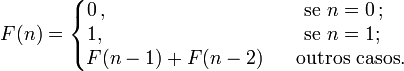Triângulo de Sierpinski

O Triângulo de Sierpinski pertence a uma classe de objectos matemáticos conhecidos como fractais, cuja principal característica é não perder a sua definição inicial à medida que é ampliado. Este triângulo foi descrito por Waclaw Sierpinski em 1915 e obtém-se como limite de um processo recursivo. Para começar o processo partimos de um triângulo equilátero. Em seguida unem-se os pontos médios de cada lado do triângulo, formando 4 triângulos cujos lados estão ligados. Retira-se agora o triângulo central. A recursão consiste em repetir indefenidamente o procedimento anterior em relação a cada um dos triângulos obtidos.

A esta sucessão de triângulos podemos associar as sucessões:

• do número de triângulos da figura:
• das áreas de cada triângulo que retiramos;
• da área total dos triângulos pintados;
• do perímetro total dos triângulos da figura.

PmatE/2007 em Aveiro

A Universidade de Aveiro dinamizou mais uma vez as competições de matemática Mat12 para os alunos do Secundário, no dia 3 de Maio. Alguns alunos do 10º e 11º anos, da Escola Fernão de Magalhães, foram seleccionados e participaram nesta competição.
A melhor classificação, da escola, foi obtida pela equipa das alunas de 11º ano Filipa Vilabril e Teresa Rei, que completaram os vinte níveis da competição e ficaram em 9º lugar.
No mesmo dia alguns alunos participaram também nas competições de Biologia Bionte.
Os resultados desta competição podem ser consultados aqui.

Números irracionais interessantes

Na história da matemática foram surgindo algumas grandezas curiosas que utilizamos com muita frequência no estudo da matemática e não só.
Vejamos algumas:

Representa o número equivalente à razão entre a circunferência e o diâmetro de um círculo, ou seja, pi (3,1415926...).
Representa em economia, taxa de inflação.
Essa letra, em maiúscula, representa um produtório (várias multiplicações em ordem, podendo representar uma progressão geométrica).

(Número de ouro)

Número de Ouro é uma constante real algébrica irracional, que há muito tempo é empregado na arte. Também é chamado de: razão áurea, razão de ouro, divina proporção, proporção em extrema razão, divisão de extrema razão.
Na história da arte renascentista a perfeição da beleza em quadros foi bastante explorada com base nesta constante. A Mona Lisa de Leonardo da Vinci utiliza o número áureo nas relações entre seu tronco e cabeça, e também entre os elementos do rosto.

Rectângulo Dourado

Proporção áurea em rectângulos
Trata-se do rectângulo no qual a proporção entre o comprimento e a largura é aproximadamente o número Phi, ou seja, 1,618.

Os Egípcios utilizaram o número de ouro nas suas construções. Por exemplo, cada bloco da pirâmide era 1,618 vezes maior que o bloco do nível a cima. As câmaras no interior das pirâmides também seguiam essa proporção, de forma que os comprimentos das salas são 1,618 vezes maior que as larguras.

(constante neperiana)

Na matemática , número de Euler , assim chamado em homenagem ao matemático suíço Leonhard Euler, é a base dos logaritmos naturais. As variantes do nome do número incluem: número de Napier, constante de Néper, número neperiano, constante matemática e número exponencial, etc. A primeira referência à constante foi publicada em 1618 na tabela de um apêndice de um trabalho sobre logaritmos de John Napier. A primeira indicação da constante foi descoberta por Jakob Bernoulli, quando tentava encontrar um valor para a seguinte expressão (muito comum no cálculo de juros compostos):

e vale aproximadamente 2,718 281 828 459 045.
O número também pode ser escrito como a soma da série infinita:

Escher

Maurits Cornelis Escher (Leeuwarden, 17 de Junho de 1898 - Hilversum, 27 de Março de 1972) foi um artista gráfico holandês conhecido pelas suas xilogravuras, litografias e meios-tons (mezzotints), que tendem a representar construções impossíveis, preenchimento regular do plano, explorações do infinito e as metamorfoses - padrões geométricos entrecruzados que se transformam gradualmente para formas completamente diferentes.
Uma das principais contribuições da obra deste artista está em sua capacidade de gerar imagens com impressionantes efeitos de ilusões de óptica, com notável qualidade técnica e estética, tudo isto, respeitando as regras geométricas do desenho e da perspectiva.
Foi numa visita à Alhambra, na Espanha, que o artista conheceu e se encantou pelos mosaicos que haviam nas mesquitas do lugar, herança das invasões árabes do passado. Escher achou muito interessantes as formas como cada figura se entrelaçava a outra e se repetia, formando belos padrões geométricos. Este foi o ponto de partida para os seus trabalhos mais impressionantes e famosos, que consistiam no preenchimento regular do plano, normalmente utilizando imagens figurativas e não geométricas, como os árabes faziam por causa da sua religião muçulmana, que proíbe tais representações.
A partir de uma malha de polígonos, regulares ou não, Escher fazia mudanças, mas sem alterar a área do polígono original. Assim surgiam figuras de homens, peixes, aves, lagartos, todos envolvidos de tal forma que nenhum poderia mais se mexer. Tudo representado num plano bidimensional.
Destacam-se também os trabalhos do artista que exploram o espaço. Escher brincava com o fato de ter que representar o espaço, que é tridimensional, num plano bidimensional, como a folha de papel. Com isto ele criava figuras impossíveis, representações distorcidas, paradoxos.

Sólidos Platónicos

Os sólidos platónicos são sólidos convexos cujas arestas formam polígonos planos regulares congruentes. A sua designação deve-se a Platão, que os descobriu no ano de 400 a.C.. A existência destes sólidos já era conhecida pelos pitagóricos, e os egípcios utilizaram alguns deles na arquitectura e noutros objectos que construíram.
Existem apenas cinco sólidos platónicos, que são os seguintes:

Estes sólidos foram adquirindo ao longo dos tempos diversos significados místicos. Por exemplo, Kepler sentia uma grande admiração e reverência por eles (Porquê apenas cinco?) e chegou mesmo a tentar explicar os movimentos planetários a partir deles. Além disso, interpretou as associações de Platão da seguinte forma:

Fractais

Fractais (do latim fractus, fração, quebrado)são figuras da geometria não-Euclidiana. A geometria fractal é o ramo da matemática que estuda as propriedades e comportamento dos fractais. Descreve muitas situações que não podem ser explicadas facilmente pela geometria clássica, e foram aplicadas em ciência, tecnologia e arte gerada por computador. As raízes conceituais dos fractais remontam a tentativas de medir o tamanho de objetos para os quais as definições tradicionais baseadas na geometria euclidiana falham. Um fractal (anteriormente conhecido como curva monstro) é um objeto geométrico que pode ser dividido em partes, cada uma das quais semelhante ao objeto original. Diz-se que os fractais têm infinitos detalhes, são geralmente auto-similares e independem de escala. Em muitos casos um fractal pode ser gerado por um padrão repetido, tipicamente um processo recorrente ou iterativo. O termo foi cunhado em 1975 por Benoît Mandelbrot, matemático francês nascido na Polónia, que descobriu a geometria fractal na década de 70 do século XX, a partir do adjetivo latino fractus, do verbo frangere, que significa quebrar.

Matemáticos

Ao longo dos anos foram diversos os matemáticos que se salientaram com a seu contributo para o desenvolvimento da matemática.

Pitágoras

Natural de Samos, na Ásia Menor, onde terá nascido nos finais do século VI a. C., emigrou para Crotona, colónia grega no Sul da Itália, e aí fundou uma escola místico-filosófica com preocupações sociopolíticas, cuja influência acabou por dominar a cidade. Atendendo ao carácter hermético da sua doutrina ( no interior da escola vigorava uma regra de sigilo que considerava como crime a divulgação dos ensinamentos aos não iniciados, pelo que não existiam quaisquer escritos), assim como à aura de profeta prodigioso que acabou por o envolver, são pouco fidedignos os relatos que dele nos chegaram, além de se tornar muito difícil distinguir o que é genuinamente de Pitágoras do que foi introduzido pelos seus discípulos.



Do interesse pela matemática resultaram alguns avanços científicos, sobretudo nas áreas da geometria e da aritmética (dos quais o Teorema de Pitágoras será o mais famoso).


Newton
Isaac Newton (Woolsthorpe, 4 de Janeiro de 1643 — Londres, 31 de Março de 1727) foi um cientista inglês mais reconhecido como físico e matemático. Foi um dos criadores, junto com Leibniz, do Cálculo Diferencial e Integral. Também descobriu várias leis da mecânica como a actualmente conhecida como Lei Fundamental da Dinâmica e a Teoria da Gravitação Universal. Para ele, a função da ciência era descobrir leis universais e enunciá-las de forma precisa e racional.
Newton estudou no Trinity College de Cambridge, tendo-se graduado em 1665. Um dos principais precursores do Iluminismo, seu trabalho científico sofreu forte influência de seu professor e orientador Barrow (desde 1663), e de Schooten, Viète, John Wallis, Descartes, dos trabalhos de Fermat sobre rectas tangentes a curvas; Cavallieri, das concepções de Galileu e Kepler.
Em 1663, formulou o teorema hoje conhecido como Binómio de Newton. Fez suas primeiras hipóteses sobre gravitação universal e escreveu sobre séries infinitas e o que chamou de teoria das fluxões (1665), o embrião do Cálculo Diferencial e Integral. Por causa da peste, o Trinity College foi fechado em 1666 e o cientista foi para casa de sua mãe em Woolsthorpe. Foi neste ano de retiro que construiu quatro de suas principais descobertas: o Teorema Binomial, o cálculo, a Lei da Gravitação Universal e a natureza das cores. Construiu o primeiro telescópio de reflexão em 1668, e foi quem primeiro observou o espectro visível que se pode obter pela decomposição da luz solar ao incidir sobre uma das faces de um prisma triangular transparente (ou outro meio de refracção ou de difracção), atravessando-o e projectando-se sobre um meio ou um anteparo branco, fenómeno este conhecido como Dispersão Luminosa. Optou, então, pela teoria corpuscular de propagação da luz, enunciando-a em (1675) e contrariando a teoria ondulatória de Huygens.

Gottfried Wilhelm Leibniz

Filósofo, matemático e conselheiro político alemão nascido em 1646, em Leipzig, e falecido em 1716, em Hanôver. Foi importante para o desenvolvimento da metafísica e da lógica, tendo-se distinguido ainda pela invenção do cálculo diferencial e integral. O seu sistema filosófico é pluralista, racionalista e optimista.

A ele é creditada a criação do termo "função" (1694), que usou para descrever uma quantidade relacionada a uma curva; como, por exemplo, a inclinação de uma curva ou um ponto qualquer de uma curva. De modo geral, juntamente com Newton, é creditado a Leibniz o desenvolvimento do cálculo moderno; em particular por seu desenvolvimento da Integral e da Regra do Produto.

Augustus de Morgan

Matemático inglês, nascido na Índia, em 1806, e falecido em 1871. Autor de inúmeros trabalhos em várias áreas da matemática, definiu e introduziu o conceito de indução matemática numa base rigorosa. Forneceu uma interpretação geométrica dos números complexos. Reconhecendo a natureza puramente simbólica da álgebra, introduziu as leis chamadas de De Morgan em lógica matemática, a sua maior contribuição para o pensamento matemático.

Leonardo Fibonacci

Matemático italiano, nascido em 1170 e falecido em 1250, natural de Pisa, foi educado no Norte de África, onde o seu pai detinha um posto diplomático. Regressado a Pisa por volta de 1200, após ter viajado extensamente, publicou Liber Abbaci, introduzindo o sistema de numeração indo-árabe. Para além deste, escreveu, ainda, Pratica Geometriae, Flos e Liber Quadratorum, de que ainda existem cópias manuscritas. Estas obras colocam Fibonacci como o maior vulto entre Diofanto e Fermat relativamente à teoria dos números, sendo construídas em torno de problemas práticos, muitos deles clássicos, mas também dirigidos à actividade mercantil característica de Pisa. A famosa sequência de números que leva o seu nome é introduzida em Liber Abacci. No entanto, para além do sistema de numeração, a influência de Fibonacci no desenvolvimento da Matemática foi mais limitada do que seria de esperar da sua obra e dos resultados atingidos.

Sucessão de Fibonacci
Na matemática, os Números de Fibonacci são uma sucessão definida por recorrência pela fórmula:

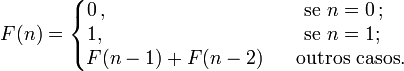
A sucessão começa com 0 e 1, e então e o próximo número de Fibonacci obtém-se somando os dois anteriores.

Os primeiros Números de Fibonacci para n = 0, 1,... são
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946

Blaise Pascal

Matemático, físico, filósofo religioso e escritor francês, nasceu em Clermont Ferrand em 1623 e morreu em Paris em 1662. Pascal foi o fundador da moderna teoria das probabilidades. As suas ideias sobre o que se encontra oculto na religião influenciaram o pensamento de Jean-Jacques Rousseau, Henri Bergson e os existencialistas. Aos 17 anos publicou um ensaio sobre matemática que lhe mereceu um elogio de René Descartes. Inventou o primeiro calculador digital (1642/1644). Realizou estudos em geometria, hidrodinâmica, hidrostática e pressão atmosférica. Inventou a seringa e descobriu a lei de Pascal da pressão (1647/1654), que se enuncia da seguinte forma: "um fluido sob determinada pressão exerce pressões totais iguais sobre iguais áreas" e o princípio da pressão hidráulica (1640). Em 1656 e 1657 empreendeu a sua famosa controvérsia com os jesuítas em 18 cartas clandestinas, conhecidas por Les Provinciales, em que Pascal coloca os problemas da teologia moral ao alcance do leitor comum, escreve a favor do jansenismo e contra os jesuítas. Devido à precisão de estilo, estas cartas marcam o início da moderna prosa francesa.

Heinrich E. Heine

Matemático alemão, Heinrich Eduard Heine nasceu em 1821 e faleceu em 1881. Foi aluno de Gauss e Dirichlet, e emprestou o seu nome ao teorema conhecido como de Heine-Borel: "um subconjunto dos reais é compacto se e só se é fechado e limitado". Foi o primeiro a formular o conceito de continuidade uniforme.
No estudo de limites de funções, no Ensino Secundário é dada uma definição de limite de função recorrendo aos limites de sucessões. É costume designá-la por definição de limite segundo
Heine, em homenagem ao matemático alemão.